하노이 탑의 규칙
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
하노이 탑은 재귀 함수로 구현하는 대표적인 문제입니다.재귀 함수란 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 방식으로 주어진 문제를 푸는 방법입니다.풀고자 하는 문제가 동일한 성격의 작은 문제들로 구성되어 있을 때 사용하면 좋습니다. 하노이 탑의 규칙으로 함수의 성격을 분석해보자
문제: N개의 원판을 1번째에서 3번째로 옮긴다.
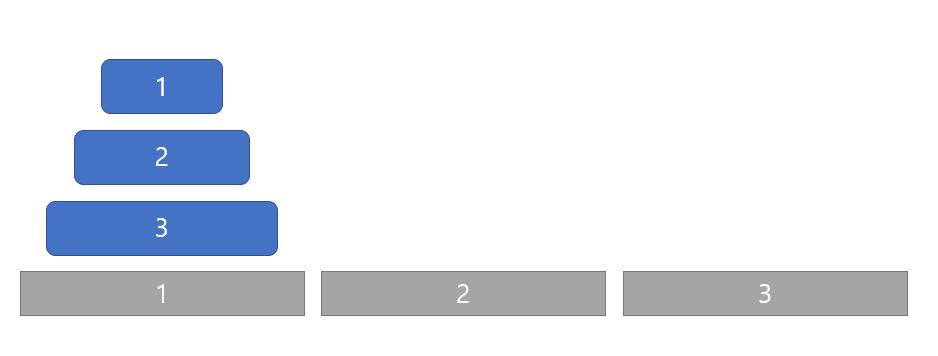
(1): N - 1개의 원판을 1번째에서 2번째로 옮긴다.
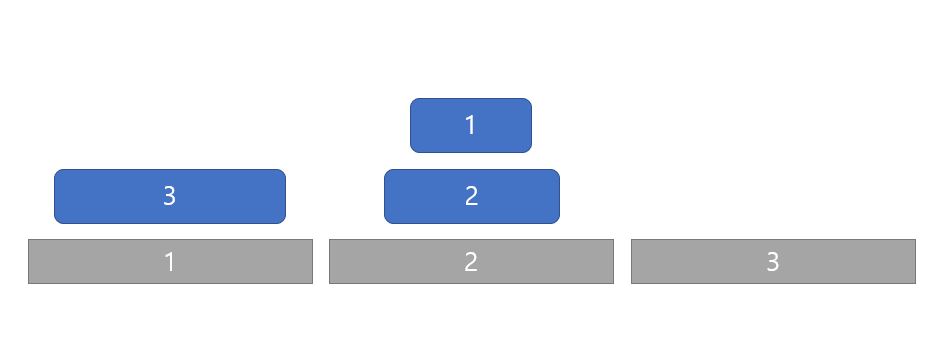
(2): N번째 원판을 1번째에서 3번째로 옮긴다.
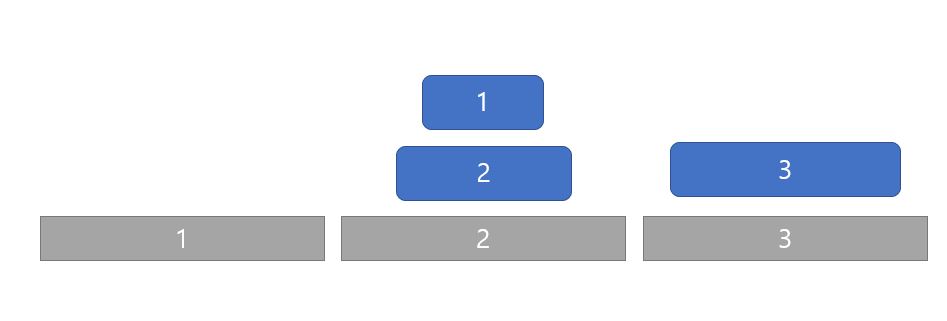
(3): N - 1개의 원판을 2번째에서 3번째로 옮긴다.
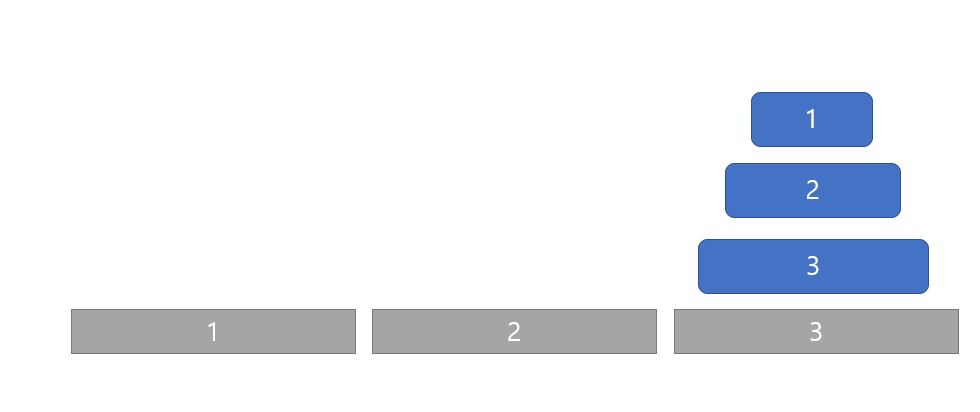
(1)과 (3) 을 보면 N의 크기만 다를 뿐 성격을 동일한 것으로 확인할 수 있습니다.
함수 원형
위의 함수의 성격을 보면 규칙에 의해 N번째 원판이 바로 1번째(from)에서 3번째(to)로 이동하지 못합니다.
N번째 원판 위에 있는 N - 1의 원판들이 2번째(by)로 잠시 이동해 있어야 N번째 원판이 자유롭게 이동이 가능하죠. N번째가 이동이 완료된 후 N - 1 원판들도 3번째(to)로 이동해줘야 합니다.
문제에서 요구하는 원판이 이동하는 횟수와 이동 방향을 출력해주기 위해 전역 변수를 선언합니다. 전역 변수를 선언하는 이유는 함수내에서 이동 방향을 바로바로 출력해줘도 되지만 문제에서 요구하는 출력 순서를 지키기 위해서는 함수가 모두 종료된 후 출력해야 합니다.
StringBuilder moveDirection = new StringBuilder();
int moveCount = 0;
public void hanoi(int n, int from, int by, int to) { }(1)
public void hanoi(int n, int from, int by, int to) {
... 생략
//(1) N번째 원판을 목적지로 옮기기 위해 N - 1 원판들을 잠시 중간다리로 옮겨두기
hanoi ( n - 1, from, to, by ); // n - 1 원판을 from - > by
... 생략
}(2)
public void hanoi(int n, int from, int by, int to) {
... 생략
//(2) N 번째 원판을 목적지로 옮기기
moveCount++; //이동 횟수 증가
moveDirection.append(from + " " + to + "\n"); //이동 방향 추가
... 생략
}(3)
public void hanoi(int n, int from, int by, int to) {
... 생략
//(3) N - 1번째 원판을 다시 목적지로 옮기기
hanoi ( n - 1, by, from, to ); // n - 1 원판을 by - > to
}재귀 함수 종료조건
(1), (2), (3) 동작을 구현함으로써 하노이 함수 동작을 모두 정의했습니다. 하지만 재귀 함수로서 가장 중요한 종료 조건이 남았습니다. 현재 프로그램을 돌리면 함수가 무한 호출되면서 메모리를 잡아먹어 Out Of Memory(OOM) ERROR를 발생합니다.
하노이 탑의 종료조건
하노이 탑의 종료조건은 옮기려는 원판의 개수가 1인 경우 입니다. N번째 원판 마지막 남은 한개의 원판이라면 자유롭게 목적지로 이동할 수 있습니다.
public void hanoi(int n, int from, int by, int to) {
//종료조건 마지막 원판일 경우 그냥 이동
if ( n == 1 ) {
moveCount++; //이동 횟수 증가
moveDirection.append(from + " " + to + "\n"); //이동 방향 추가
return;
}
... 생략
}총 하노이 탑 코드
StringBuilder moveDirection = new StringBuilder();
int moveCount = 0;
public void hanoi(int n, int from, int by, int to) {
//종료조건 마지막 원판일 경우 그냥 이동
if ( n == 1 ) {
moveCount++; //이동 횟수 증가
moveDirection.append(from + " " + to + "\n"); //이동 방향 추가
return;
}
//(1) N번째 원판을 목적지로 옮기기 위해 N - 1 원판들을 잠시 중간다리로 옮겨두기
hanoi ( n - 1, from, to, by ); // n - 1 원판을 from - > by
//(2) N 번째 원판을 목적지로 옮기기
moveCount++; //이동 횟수 증가
moveDirection.append(from + " " + to + "\n"); //이동 방향 추가
//(3) N - 1번째 원판을 다시 목적지로 옮기기
hanoi ( n - 1, by, from, to ); // n - 1 원판을 by - > to
}'Algorithm_Java' 카테고리의 다른 글
| [알고리즘] 백준 12865 - 평범한 배낭 (0) | 2020.07.16 |
|---|---|
| [알고리즘] 백준 2565 - 전깃줄 (0) | 2020.07.12 |
| [알고리즘] 백준 2580 - 스도쿠 (0) | 2020.06.22 |
| [알고리즘] 백준 1929 소수 구하기 - 에라토스테네스의 체 (0) | 2020.06.02 |
| 완전 탐색 By 재귀 호출 ( 프로그래머스 - 소수 찾기 ) (0) | 2020.02.04 |
